Lecture 2: Supervised Learning of Behaviors

Lecture Slides & Videos

• Lecture 2: Supervised Learning of Behaviors

• CS 285: Lecture 2, Imitation Learning. Part 1

• CS 285: Lecture 2, Imitation Learning. Part 2

• CS 285: Lecture 2, Imitation Learning. Part 3

• CS 285: Lecture 2, Imitation Learning. Part 4

• CS 285: Lecture 2, Imitation Learning. Part 5

Abstract

• Imitation learning vis behavioral cloning is not guaranteed to work
  • This is different from supervised learning
  • The reason: i.d.d. assumption does not hold!
• We can formalize why this is and do a bit of theory
• We can address the problem in a few ways:
  • Be smart about how we collect ( and augment ) out data
  • Use very powerful models that make very few mistakes
  • Use multi-tasks learning
  • Change the algorithm ( DAgger )

Terminology & notation

$\mathbf{s}_t$ — state ( $\mathbf{x}_t$ sometimes )

$\mathbf{o}_t$ — observation

$\mathbf{a}_t$ — action ( $\mathbf{u}_t$ sometimes )

$\pi_\theta(\mathbf{a}_t | \mathbf{o}_t)$ — policy

$\pi_\theta(\mathbf{a}_t | \mathbf{s}_t)$ — policy ( fully observed )

$r(\mathbf{s}_t, \mathbf{a}_t)$ — reward function ( $c(\mathbf{s}_t, \mathbf{a}_t)$ as the cost function )

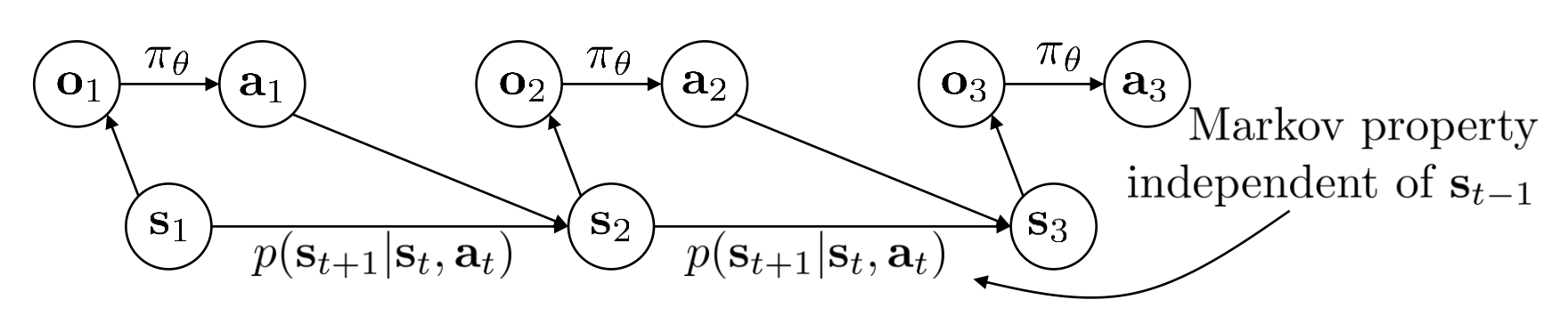
Imitation Learning

Behavioral Cloning

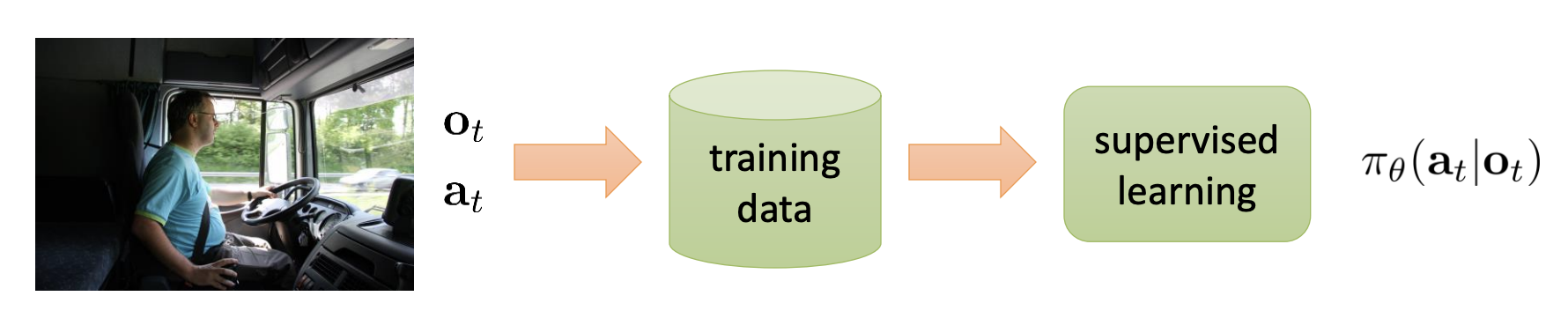
Behavioral Cloning is the essence of the most basic kind of imitation learning method. But it usually doesn’t work well.

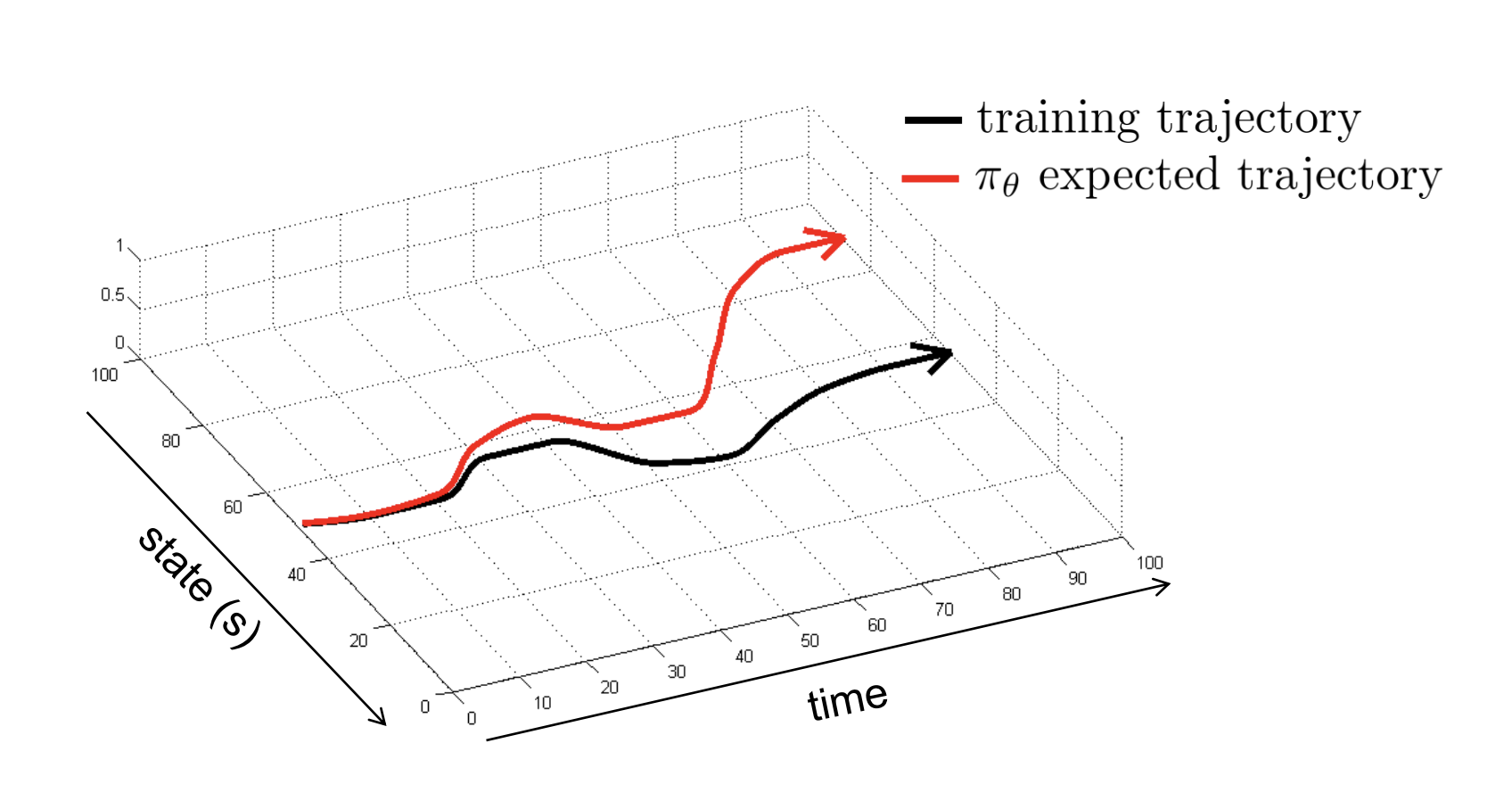
When some mistakes happen, the policy will meet a state that is different from the one seen in the training process. That makes the mistakes to accumulate, leading the policy trajectory to a very wrong ending.

It doesn’t happen in regular supervised learning because of the i.i.d. property, which assume that each training points doesn’t affect the other training points.

Why does the behavioral cloning fail? — A bit of theory

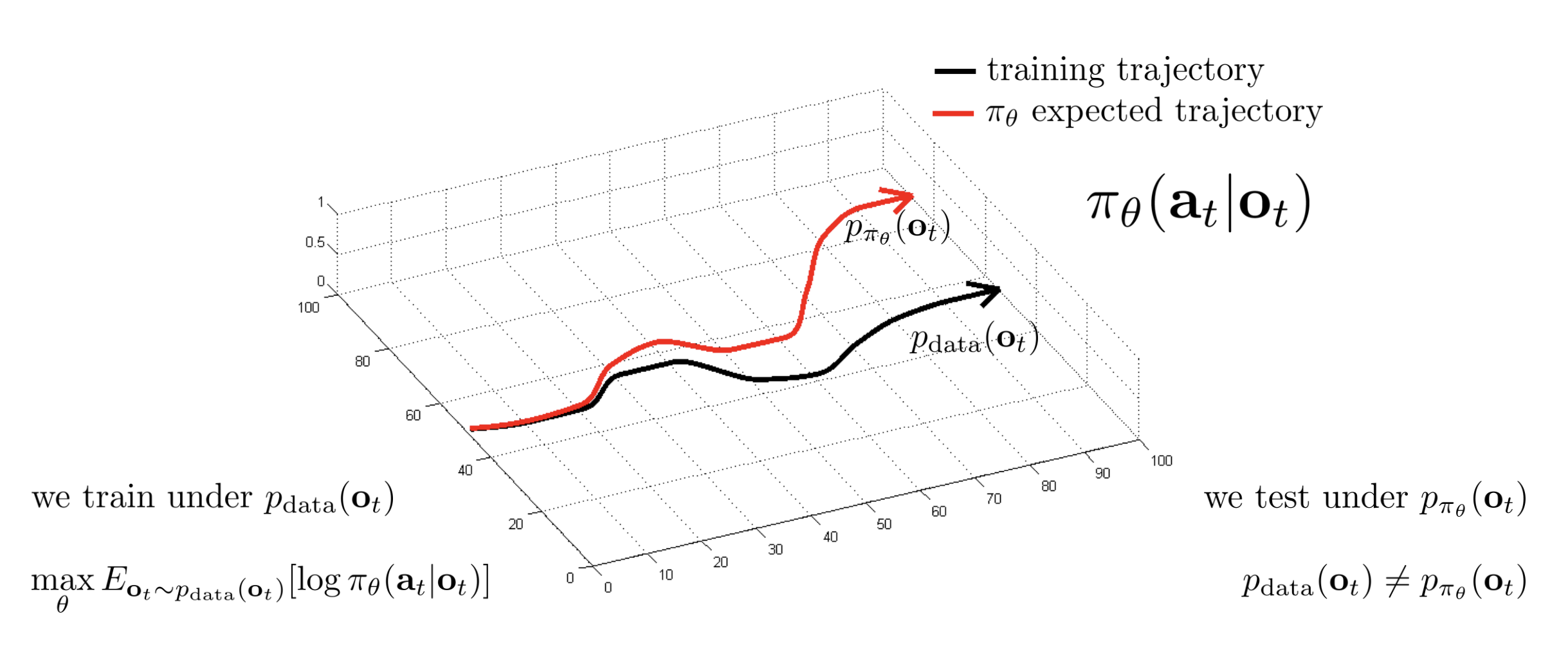
We train a policy $\pi_\theta(\mathbf{a}_t | \mathbf{o}_t)$ under training trajectory $p_{data}(\mathbf{o}_t)$ using supervised maximum likelihood:

$$ \max_\theta E_{\mathbf{o}_t\sim p_\mathrm{data}(\mathbf{o}_t)}[\log\pi_\theta(\mathbf{a}_t|\mathbf{o}_t)] $$

The problem is, when we test under $p_{\pi_\theta}(\mathrm{o}_t)$, we can expect the difference between $p_{\pi_\theta}(\mathrm{o}_t)$ and $p_{data}(\mathrm{o}_t)$, since they are different, which is often referred as distributional shift. It means that the distribution under which the policy is tested is shifted from the distribution under which it’s trained.

What makes a learned $\pi_\theta(\mathbf{a}_t | \mathbf{o}_t)$ good or bad?

It probably shouldn’t be the likelihood of the training actions due to the distributional shift.

One measure we can use, for example in a self-driving case, might be as follow:

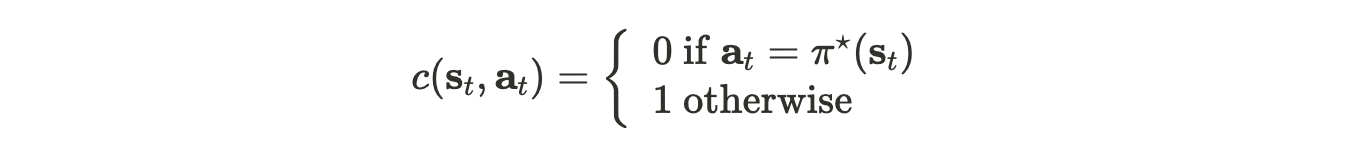
and we try to minimize $E_{\mathbf{s}t\thicksim p{\pi_\theta}(\mathbf{s}_t)}[c(\mathbf{s}_t,\mathbf{a}_t)]$.

The point here is that what we care about is the number of mistakes that the policy makes when it’s actually drives the car, and we don’t really care how many mistakes it would make when it’s looking at what the humans’ images.

That means, what we care about is the cost in expectation under $p_{\pi_\theta}$, under the distribution of states that the policy will actually see.

• More analysis

  

  

In general, you could imagine that with these accumulating errors, if instead of training on fairly narrow and optimal trajectories, but training on a set of trajectories that all make some mistakes and then recover from the mistakes such that the training distribution is a little bit broader so that whenever you make a small mistake you’re still in distribution, then your policy might actually learn to correct those mistakes and still do fairly well.

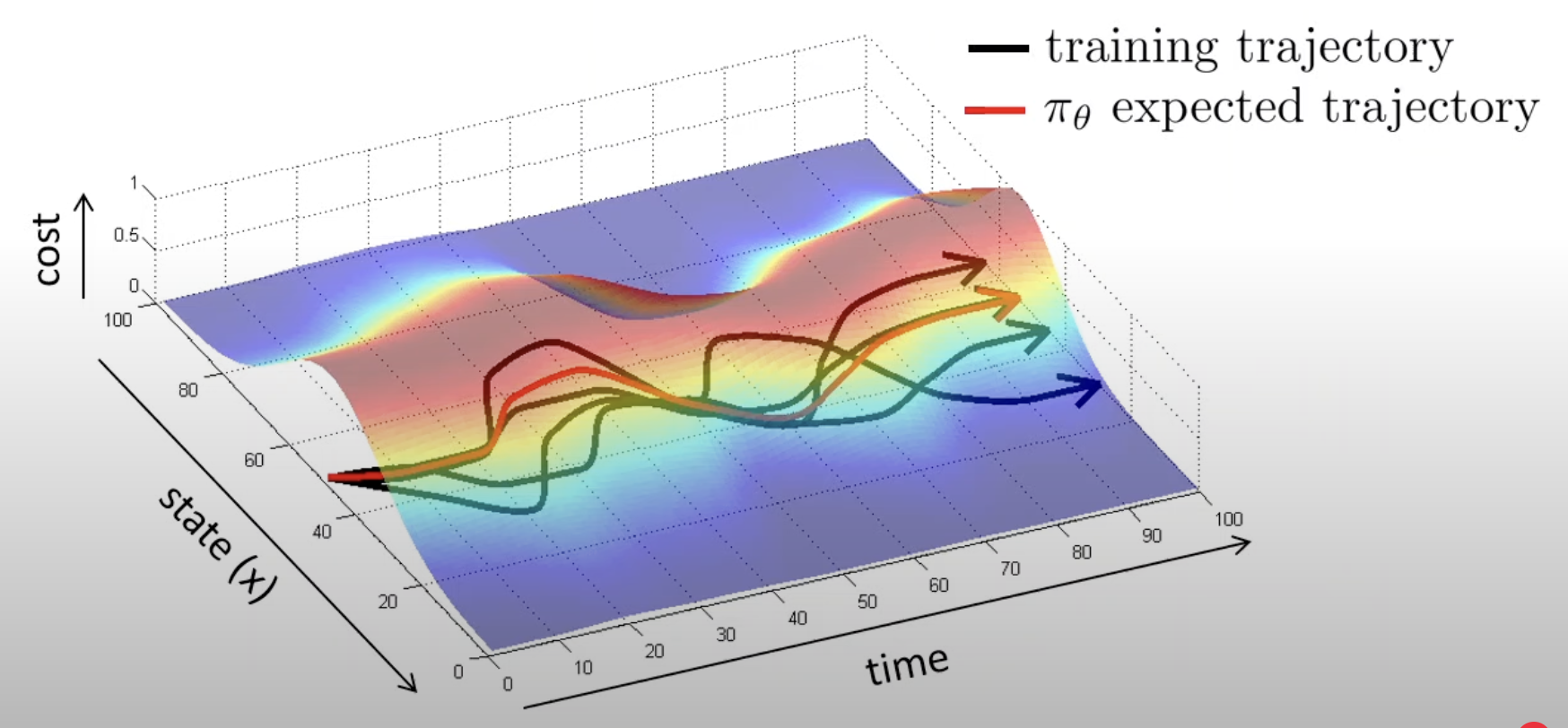
A paradox: imitation learning can work better if the date has more mistakes (and recoveries).

Why might we fail to fit the expert?

• Non-Markovian behavior

  • $\pi_\theta(\mathbf{a}_t | \mathbf{o}_t)$ : behavior depends only on current observation
  • $\pi_\theta(\mathbf{a}_t | \mathbf{o}_1, … ,\mathbf{o}_t)$ : behavior depends on all past observations

  How can we use the whole history?

  

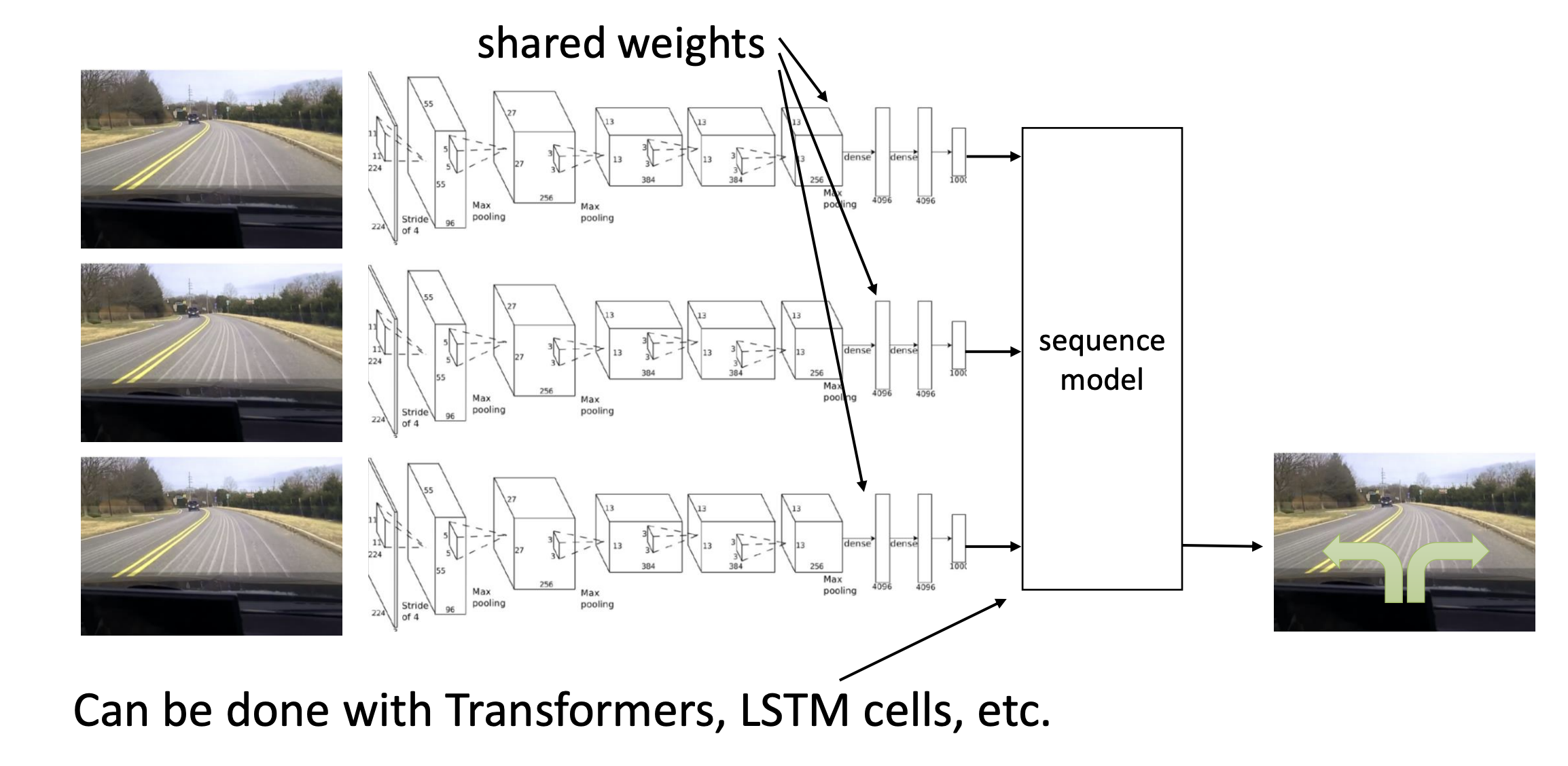
  • Aside: why might this work poorly?

    

• Multimodel behavior

  ( This is also mentioned in paper Diffusion Policy: Visuomotor Policy Learning via Action Diffusion by Cheng Chi.)

  If we are outputting a continuous action, maybe the mean and variance of the a Gaussian distribution, we will get a problem since a Gaussian has only one mode. We may average examples of left and examples of right, which is really really bad.

  

  • More expressive continuous distributions.

    • mixture of Gaussian

      

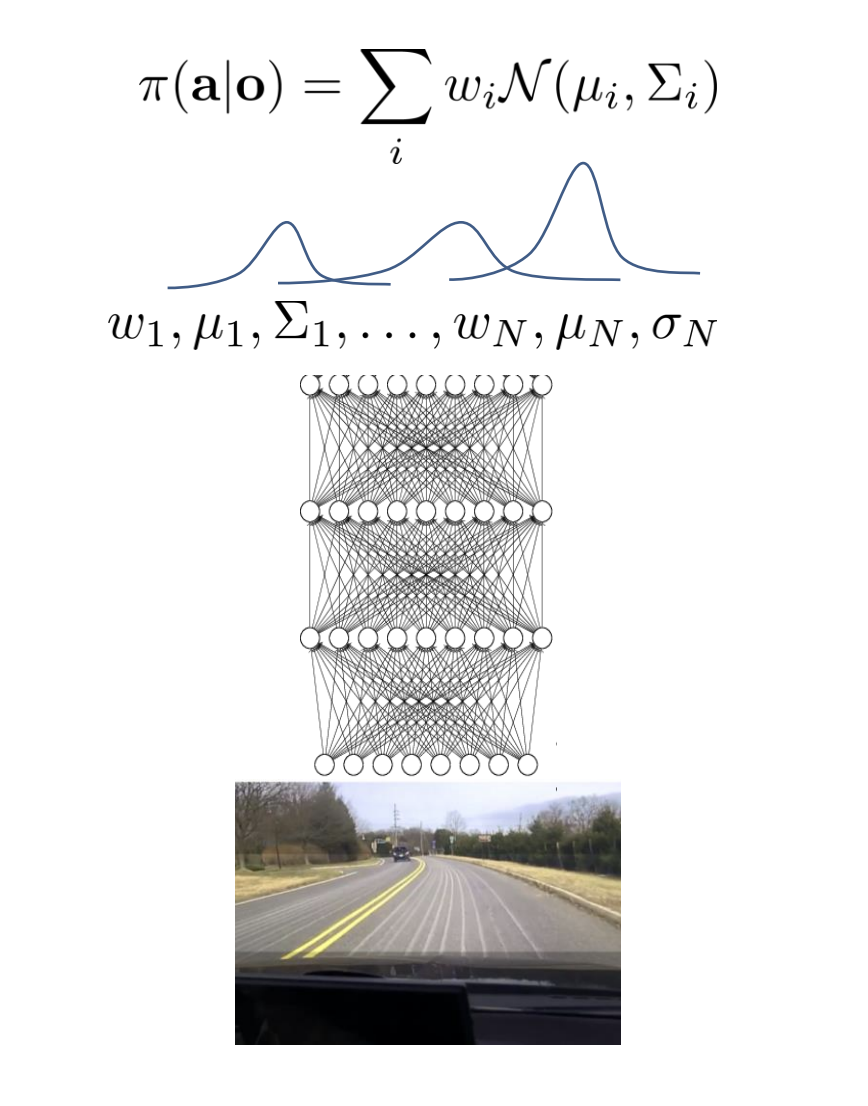
    • latent variable models

      

    • diffusion models

      

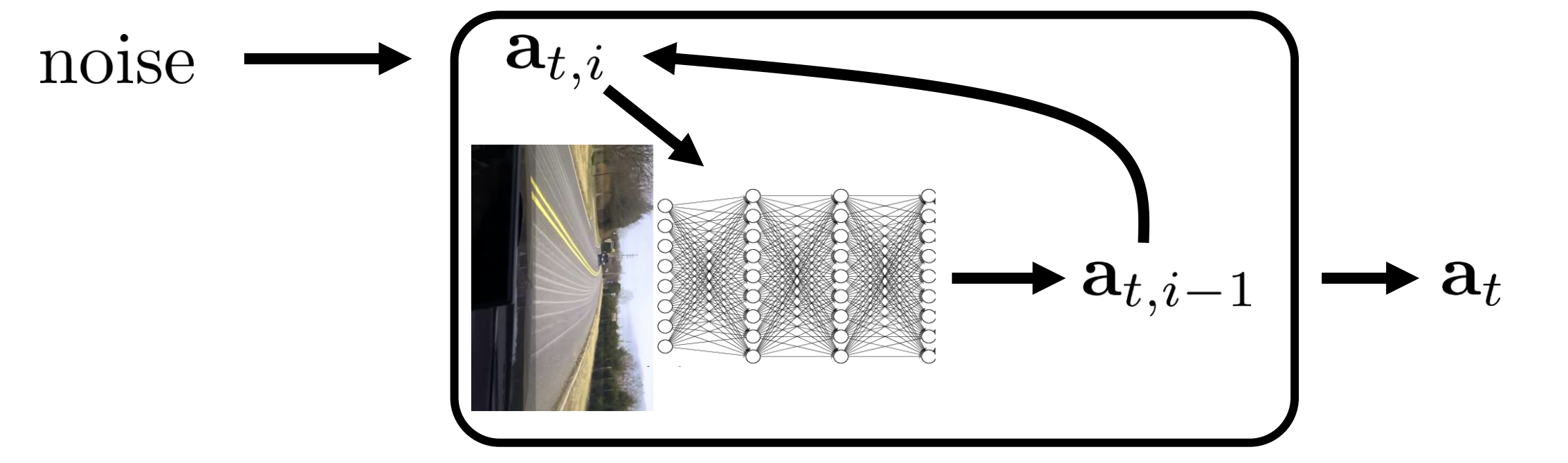
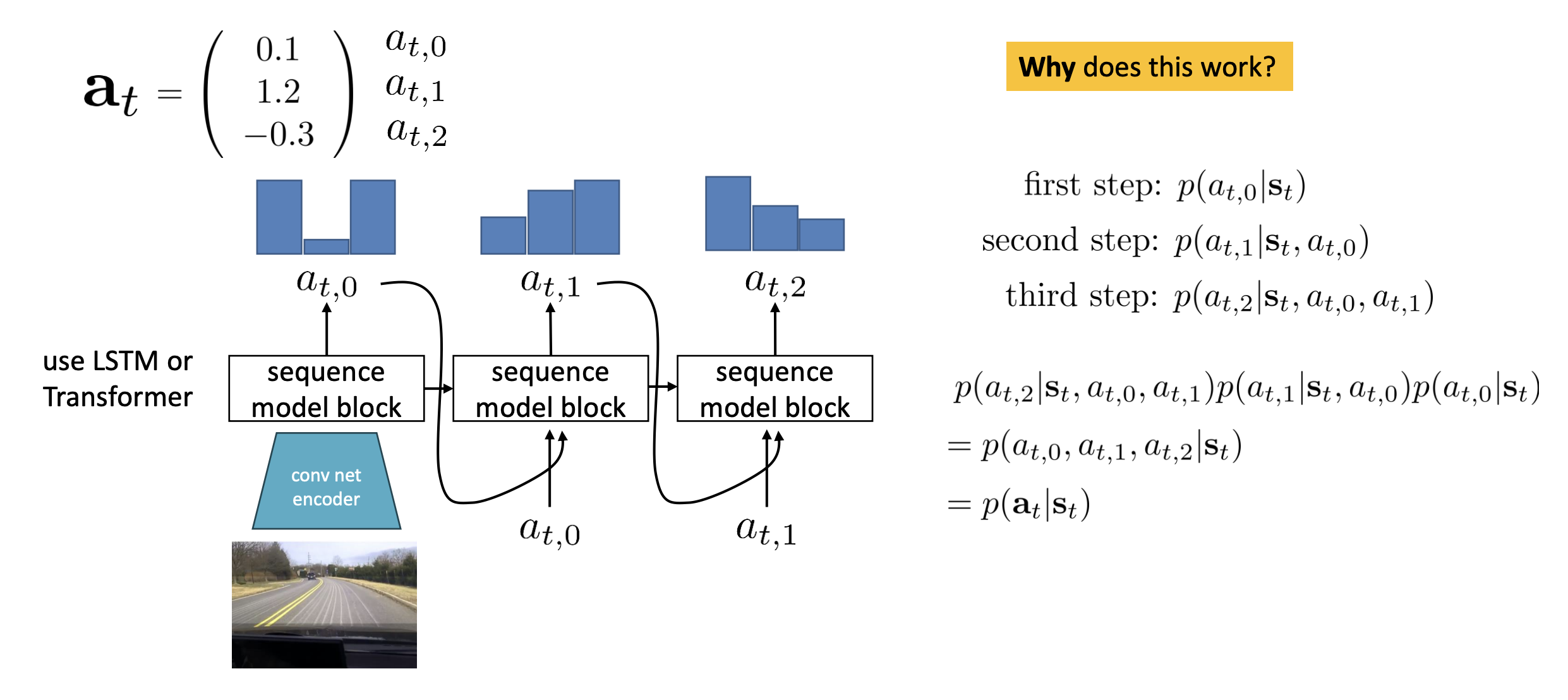
  • Discretization with high-dimensional action space.

    • Problem: This is great for 1D actions, but in higher dimensions, discretizing the full space is impractical.

      Solution: discretize one dimension at a time

    • Autoregressive discretization

      

Does learning many tasks became easier?

Goal-conditioned behavioral cloning

demo 1: ${\mathbf{s}_1,\mathbf{a}_t,\ldots,\mathbf{s}_{T-1},\mathbf{a}_{T-1},\mathbf{s}_T}$

demo 2: ${\mathbf{s}_1,\mathbf{a}_t,\ldots,\mathbf{s}_{T-1},\mathbf{a}_{T-1},\mathbf{s}_T}$ $\Rightarrow$ learn $\pi_\theta(\mathbf{a} | \mathbf{s}, \mathbf{g})$, where $\mathbf{g}$ stands for the goal state

demo 3: ${\mathbf{s}_1,\mathbf{a}_t,\ldots,\mathbf{s}_{T-1},\mathbf{a}_{T-1},\mathbf{s}_T}$

for each demo, maximize $\log\pi_\theta(\mathbf{a}_t^i|\mathbf{s}_t^i,\mathbf{g}=\mathbf{s}_T^i)$

One of the interesting things you could do with these goal-conditional behavioral cloning methods is that you can actually use them as online self-improvement methods, very similar in spirit to RL.

• Start with a random policy
• Collect data with random goals
• Treat this data as “demonstrations” for the goals that were reached
• Use this to improve the policy
• Repeat

Goal-conditional behavioral cloning methods are quite scalable.

Can we make it work more often?

Can we make $p_{data}(\mathbf{o}_t) = p_{\pi_\theta}(\mathbf{o}_t)$ ?

idea: instead of being clever about $p_{\pi_\theta}(\mathbf{o}_t)$, be clever about $p_{data}(\mathbf{o}_t)$!

DAgger: Dataset Aggregation

$\Rightarrow$ run the policy in the real world, see which states it visits and ask humans to label those states

goal: collect training data from $p_{data}(\mathbf{o}_t)$ instead of $p_{data}(\mathbf{o}_t)$

how? just run $\pi_\theta(\mathbf{a}_t | \mathbf{o}_t)$, but need labels $\mathbf{a}_t$!

• Train $\pi_\theta(\mathbf{a}_t | \mathbf{o}_t)$ from human data $\mathcal{D} = {\mathbf{o}_1, \mathbf{a}_1, …, \mathbf{o}_N, \mathbf{a}_N}$
• Run $\pi_\theta(\mathbf{a}_t | \mathbf{o}_t)$ to get dataset $\mathcal{D}_\pi = {\mathbf{o}_1,…,\mathbf{o}_M}$
• Ask human to label $\mathcal{D}_\pi$ with action $\mathbf{a}_t$
• Aggregate: $\mathcal{D}\leftarrow\mathcal{D}\cup\mathcal{D}_\pi$
• Repeat

Imitation learning: what’s the problem?

• Humans need to provide data, which is typically finite
  • Deep learning works best when data is plentiful
• Humans are not good at providing some kind of actions
  • e.g. controlling the low-level commands
• Humans can learn autonomously; can our machines do the same?
  • Unlimited data from own experience
  • Continuous self-improvement